Trig: The Pitch of a Roof
When developers are constructing houses, they must account for the roof.
When constructing these roofs, the word pitch is used to assess the incline. The term "pitch" is another type of measurement that is expressed when using slope. Like grade, it determines the steepness of a slope, but instead of measuring roads, pitch measures the steepness of roofs. Like grade and slope, to determining pitch is quite simple. You take the rise over run. When finding the angle of elevation of a roof when given its pitch, you simply take the inverse tangent and multiply it by the pitch.
For example, a terracotta roof vertically "rises" 11 inches for every 18 inches horizontally "run". This means the pitch of the roof would be 11/18. What would the angle of elevation of the roof be? To solve this problem and find the angle of elevation, you simply take the inverse tangent and multiply it by the pitch.
If following steps above, you should get the answer of 31 degrees.
In addition to finding the pitch and angle of elevation of the roof, the total run of the rafter line is 22ft. Given this length, what would the total rise and length of rafter be?
To find the rise of the rafter, you can either multiply the "run" by the pitch, or alternatively calculate the rise by looking at similar triangles. Both methods are shown above.
The length of the rafter is found by the equation: Length of rafter =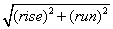
The example of this is shown below:
In the end, tangent relates to "pitch", "grade" and "slope" because you need it in order to find values such as the rise and run, opposite sides, adjacent sides, and the angle of elevation. Tangent is one of the most important elements when determining pitch.
When constructing these roofs, the word pitch is used to assess the incline. The term "pitch" is another type of measurement that is expressed when using slope. Like grade, it determines the steepness of a slope, but instead of measuring roads, pitch measures the steepness of roofs. Like grade and slope, to determining pitch is quite simple. You take the rise over run. When finding the angle of elevation of a roof when given its pitch, you simply take the inverse tangent and multiply it by the pitch.
For example, a terracotta roof vertically "rises" 11 inches for every 18 inches horizontally "run". This means the pitch of the roof would be 11/18. What would the angle of elevation of the roof be? To solve this problem and find the angle of elevation, you simply take the inverse tangent and multiply it by the pitch.
If following steps above, you should get the answer of 31 degrees.
In addition to finding the pitch and angle of elevation of the roof, the total run of the rafter line is 22ft. Given this length, what would the total rise and length of rafter be?
The length of the rafter is found by the equation: Length of rafter =
The example of this is shown below:
In the end, tangent relates to "pitch", "grade" and "slope" because you need it in order to find values such as the rise and run, opposite sides, adjacent sides, and the angle of elevation. Tangent is one of the most important elements when determining pitch.
Comments
Post a Comment